字符串之KMP算法

Posted on | In

字符串匹配的算法也可以说是刷题之路的老大难了，特别是KMP算法，每次遇到类似的题都去学习KMP算法，好像每次也只是看懂KMP的步骤，并没有自己实现过。

今天我来实现下，希望把这个实现当成自己的KMP模板后面写子串的匹配问题可以信手拈来。

这篇blog并不会去详细说明kmp怎么来的，以及什么next要这么实现。

KMP 算法（Knuth-Morris-Pratt 算法）是一个著名的字符串匹配算法 。

关于字符串匹配我们首先最容易想到的就是暴力匹配。

为了方便描述问题，我们先引出一道例题。

Leetcode 28. 实现 strStr()

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:

1
2
3
> 输入: haystack = "hello", needle = "ll"
> 输出: 2
>

示例 2:

1
2
3
> 输入: haystack = "aaaaa", needle = "bba"
> 输出: -1
>

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

例题中给的两个例子对于描述KMP算法来说不够直观，为了描述的统一性，我们选取两个串。

T = “abaacababcac”

P = “ababc”

暴力匹配

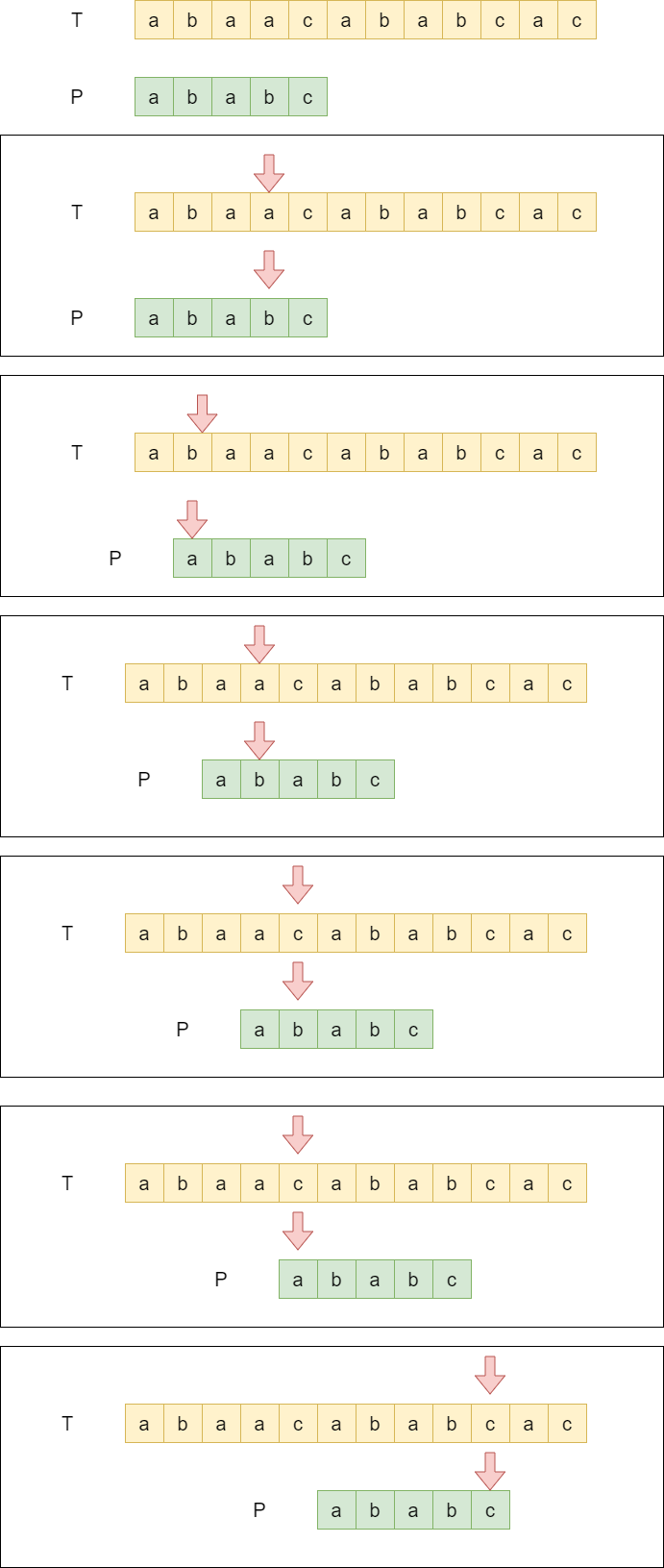
用暴力匹配的方法我们怎么去匹配上面两个串呢?

很简单我们每次选取T的第一个字符与P的第一个字符进行比较，若P中所有的字符都与T串中的字符匹配则找到答案。

暴力算法是如果P中的字符与T中的字符不同，需要将指向T的指针向前移动一位，而指向P的指针需要回退到起点，然后再从新进行匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int strStr(const string& haystack, const string& needle) {
        // bf
        if (needle.empty()) return 0;		// 空串返回0
        int m = haystack.size(), n = needle.size();
        // 当两个串长度相同的时候
        if (m == n) return (haystack == needle) ? 0 : -1;
        for (int i = 0; i <= m - n; ++i){
            int j = 0;
            for (; j < n; ++j){
                if (haystack[i + j] != needle[j])
                    break;
            }
            if (j == n) return i;
        }
        return -1;
    }
};

暴力匹配最大的问题就是当

T = “aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab”

P = “aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab”

这种极端的情况下，使得算法的时间复杂度过高.

暴力匹配的时间复杂度为: O(M*N)，其中M为T串的长度，N为P串的长度。

KMP算法

KMP 算法的不同之处在于，它会花费空间来记录一些信息，不至于当遇到T[i] != P[j]，j直接回退到起点0。

KMP算法主要借助了一个叫next数组的东西.

next数组怎么求的呢?

从P串中求真前缀与后缀的相同子串的长度.

例如: P = “ababc”

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> next_arr;
void get_next(const string& P) {
	int len = P.size();
	next_arr.assign(len + 1, 0);
	int j = next_arr[0] = -1;
	for (int i = 0; i < len; ) {
        // 当j != -1 并且真后缀的下标与前缀的下标不同
		while (j != -1 && P[j] != P[i])
			j = next_arr[j];
		next_arr[++i] = ++j;
	}
}

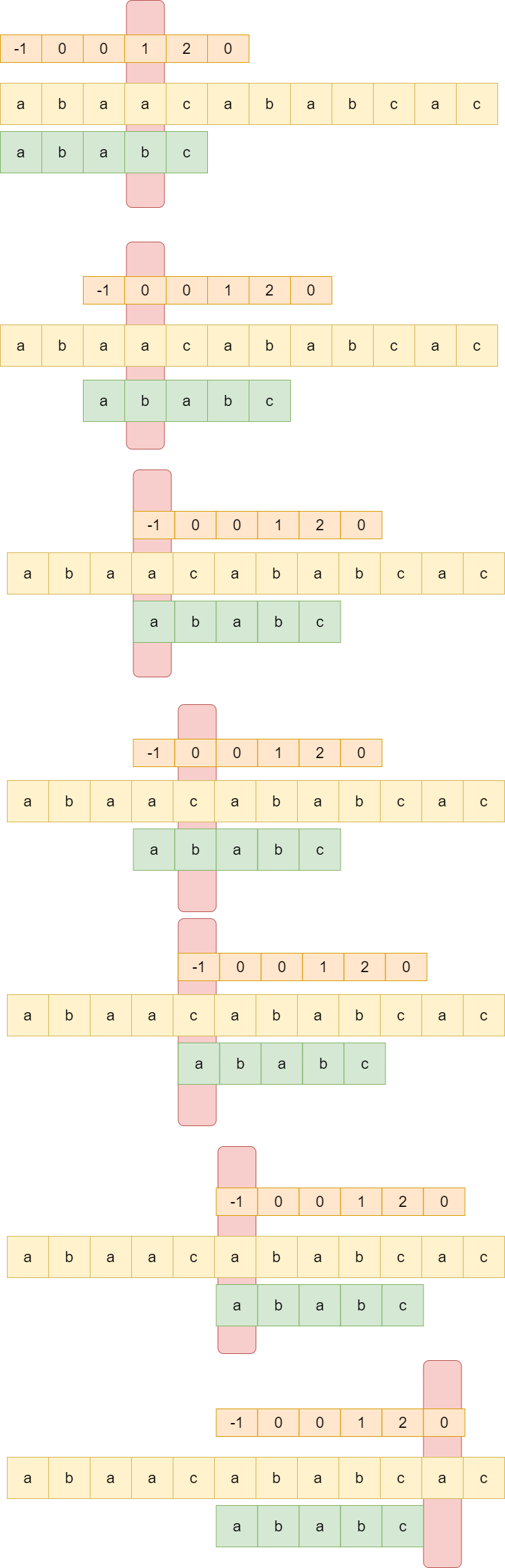
kmp算法在匹配时会参考next数组，使得每次P串在匹配的时候不至于从0开始匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int strStr(string haystack, string needle) {
        int m = haystack.size(), n = needle.size();
        get_next(needle);
        int i = 0, j = 0;
        for (; i < m && j < n; ++i, ++j){
            while (j != -1 && haystack[i] != needle[j])
                j = next_arr[j];
        }
        return j == n ? i - n : -1;
    }

    vector<int> next_arr;
    void get_next(const string& P) {
        int len = P.size();
        next_arr.assign(len + 1, 0);
        int j = next_arr[0] = -1;
        for (int i = 0; i < len; ) {
            while (j != -1 && P[j] != P[i])
                j = next_arr[j];
            next_arr[++i] = ++j;
        }
    }
};

KMP算法根据分摊平均时间复杂度为O(M)

参考:

正月点灯笼