剑指offer 51.数组中的逆序对

Posted on | In

记得考研一战华科软院的时候，华科专业课也出过这个题，当时还强调要求写出时间复杂度为O(n*logn)，看网上人家写的答案那叫一个懵逼啊。

今天有幸把这题做出来，顺带纪念下青春吧。

剑指 Offer 51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

1
2
3
> 输入: [7,5,6,4]
> 输出: 5
>

限制：

1
2
> 0 <= 数组长度 <= 50000
>

暴力法

思路: 暴力法是很容易想到的方法，把当前元素逐个的与后续的元素比较，若当前元素大于后续元素则构成逆序对。

时间复杂度为O(n^2)，一般的OJ平台是会TLE的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int reversePairs(vector<int>& nums) {
        // 当数组中的元素数量小于2的时候说明不可能存在逆序对
        if (nums.size() < 2)    return 0;
        int cnt = 0;
        for (int i = 0;i < nums.size(); ++i){
            for (int j = i + 1;j < nums.size(); ++j){
                if (nums[i] > nums[j])  cnt++;
            }
        }
        return cnt;
    }
};

分治

由于暴力法并没有记录上次遍历有关的信息，所以在下次遍历的过程中又重新遍历一次。

我们可以通过什么方法来减少遍历的次数呢？利用阶段性的信息去逐渐得到最终的结果。

这道很经典的问题可以用归并排序的方式来解决。

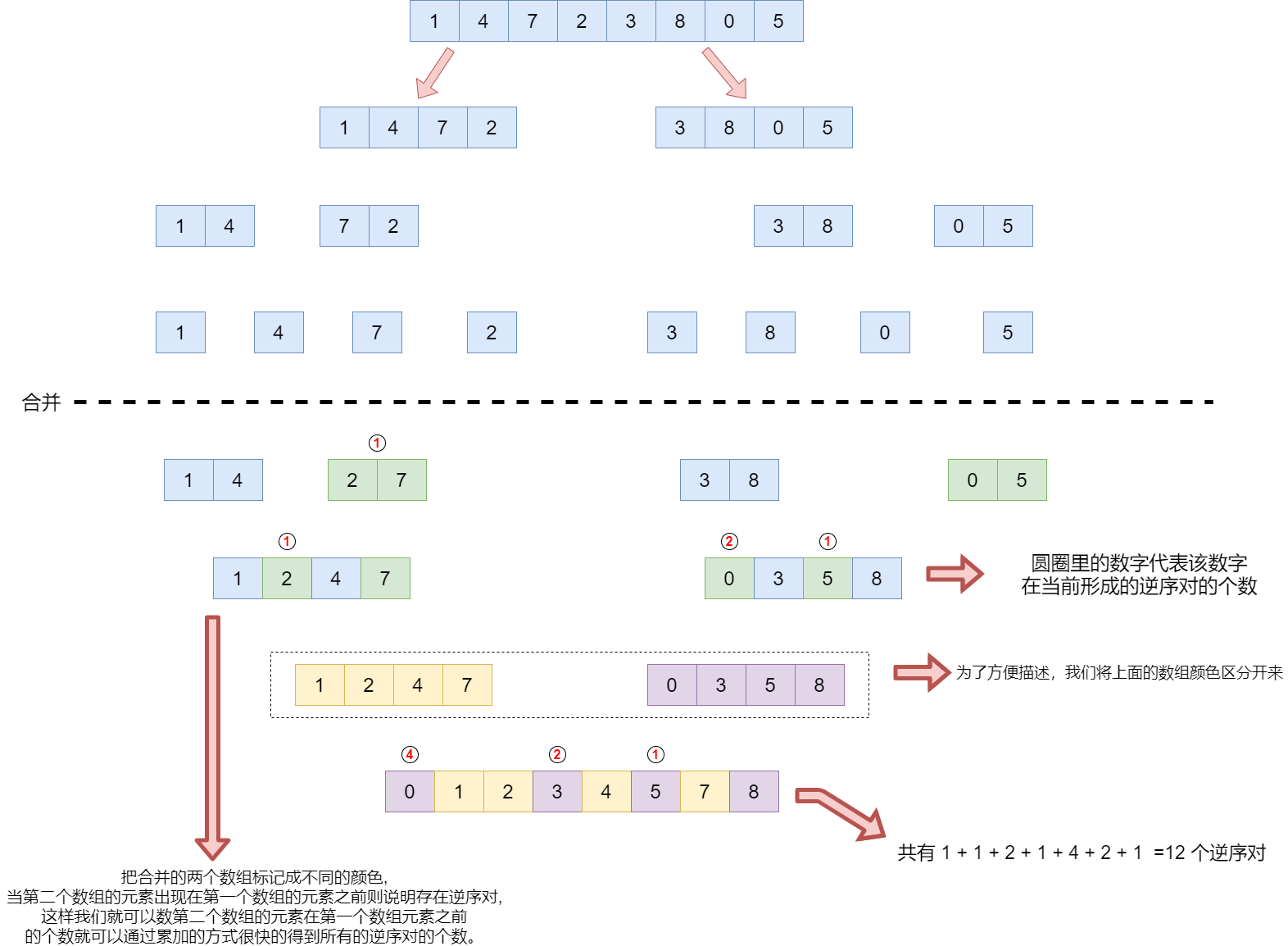
我们以[1,4,7,2,3,8,0,5]为例子，通过下图来看看如何做到的实现统计逆序对。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    int reversePairs(vector<int>& nums) {
        if (nums.size() < 2)    return 0;
        return reversePairs(nums, 0, nums.size() - 1);
    }

    int reversePairs(vector<int>& nums, int l, int r){
        if (l >= r) return 0;   // 递归终止条件
        int mid = l + (r - l) / 2;
        // [l ... r] ==> [l ... mid] && [mid+1 ... r]
        int l_cnt = reversePairs(nums, l, mid);         // 左边有多少个逆序对
        int r_cnt = reversePairs(nums, mid + 1, r);     // 右边有多少个逆序对
        int cnt = merge(nums, l, mid, r);               // 左右合并有多少个
        return l_cnt + r_cnt + cnt;         
    }

    int merge(vector<int>& nums, int l, int mid, int r){
        vector<int> tmp(r - l + 1, 0);
        int i = l, j = mid + 1, k = 0, cnt = 0;
        while (i <= mid || j <= r){
            if (i <= mid && j <= r){
                if (nums[i] <= nums[j])
                    tmp[k++] = nums[i++];
                else{
                    // 当后面的数组的数字小于前面数组的数字时候出现逆序对
                    tmp[k++] = nums[j++];
                    cnt += (mid - i) + 1;
                }
            }
            else if (i <= mid)
                 tmp[k++] = nums[i++];
            else
                tmp[k++] = nums[j++];
        }
        // 将归并好的数组还原到原数组
        for (int i = 0, j = l; i < tmp.size() && j <= r; ++i, ++j)
            nums[j] = tmp[i];
        return cnt;
    }
};