LeetCode 85.最大矩形

Posted on | In

继LeetCode 84题这题延续了84的思想，算是84题的变种吧。

也是一道很经典的单调栈的题，值得反复回味。

85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

1
2
3
4
> 输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
> 输出：6
> 解释：最大矩形如上图所示。
>

示例 2：

1
2
3
> 输入：matrix = []
> 输出：0
>

示例 3：

1
2
3
> 输入：matrix = [["0"]]
> 输出：0
>

示例 4：

1
2
3
> 输入：matrix = [["1"]]
> 输出：1
>

示例 5：

1
2
3
> 输入：matrix = [["0","0"]]
> 输出：0
>

提示：

  • rows == matrix.length
  • cols == matrix[0].length
  • 0 <= row, cols <= 200
  • matrix[i][j] 为 ‘0’ 或 ‘1’

思路: 这题的思想和LeetCode 84.柱状图中最大的矩形很类似。

可以把这题转化成第84题，首先我们观察题目中给出的例图。

我们先从第0行开始看，由于它上面没有其他行，保留该行的所有数据。

我们再观察第一行，它上面有第一行，若同一列上有大于0的值，我们把它累加起来，但如果我们现在遍历的元素值本身为0，则不累加，这样就可以转化为下面这个图。其中标红的就是最大的面积值(宽为3, 高为2).

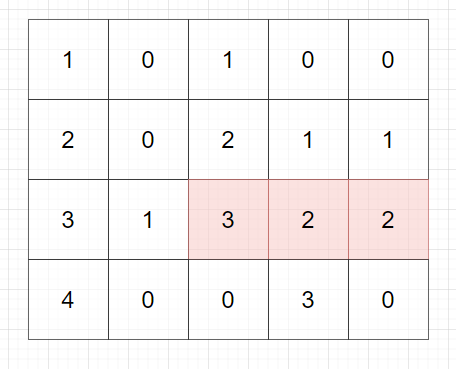
然后每一行都可以看成第84题，相当于我们现在做的这个题是在第84题的基础上，加了一个维度。

然后我们需要求出最大值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty()) return 0;
        int rows = matrix.size(), cols = matrix[0].size();
        vector<vector<int>> tmp(rows, vector<int>(cols, 0));
        // 处理第0行
        for (int j = 0; j < cols; ++j)
            tmp[0][j] = matrix[0][j] - '0';
        // 处理后续
        for (int i = 1; i < rows; ++i){
            for (int j = 0; j < cols; ++j){
                if (matrix[i][j] == '0')    tmp[i][j] = 0;
                else
                    tmp[i][j] = tmp[i - 1][j] + 1;
            }
        }

        // 为了简化代码 ==> 在tmp左右两端插入两个全为0的柱子!
        vector<vector<int>> n_matrix(rows, vector<int>(cols + 2, 0));
        for (int i = 0; i < rows; ++i)
            for (int j = 0, k = 1; j < cols; ++j, ++k)
                n_matrix[i][k] = tmp[i][j];
        // 现在开始求解每一行中最大的矩阵面积 (我们需要一个84题解的函数)
        // 二维的84题
        int ans = 0;
        for (int i = 0 ; i < rows; ++i)
            ans = max(ans, max_rect(n_matrix, i));
        return ans;
    }

    int max_rect(vector<vector<int>>& n_matrix, int cur_row){
        stack<int> st;
        int ret = 0;
        for (int j = 0; j < n_matrix[0].size(); ++j){
            while (!st.empty() && n_matrix[cur_row][j] < n_matrix[cur_row][st.top()]){
                int cur_h = n_matrix[cur_row][st.top()];
                st.pop();
                int area = cur_h * (j - st.top() - 1);
                ret = max(ret, area);
            }
            st.push(j);
        }
        return ret;
    }
};