LeetCode 84.柱状图中最大的矩形

Posted on | In

自己思考很久都没头绪的题，看了甜姨的题解之后豁然开朗。

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。


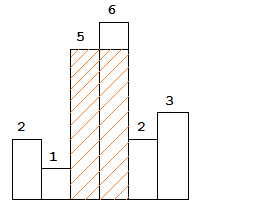
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。
示例:

1
2
3
> 输入: [2,1,5,6,2,3]
> 输出: 10
>

思路: 这题就是在考察用什么方法才能找到最大的面积。

我们先给出结论：遍历每一根柱子分别向左右两个方向找第一个小于该柱子的柱子，然后以找到的两个值的横坐标为之差就为当前柱子能够形成最大矩形面积的宽（例如左边柱子的横坐标为l, 右边柱子横坐标为r, 那么宽度就为 「r - l - 1」），乘以当前这个柱子的高度，即为这个柱子能够在柱状图中形成的最大面积，最后通过比对求出柱状图中的最大矩形。

下面我们来举一个例子来验证，我上面说的结论。

柱状图的初始状态

##### 我们分别来看看下标[0, 1, ,2, 3, 4, 5, 6]能够形成的最大矩形的面积

下标为0的柱子能形成的最大矩阵的面积为(3 + 1 - 1 ) * 5 (这里为什么是加1呢?因为我们假设0左边的下标为-1,且高度为0。同理，下标6左边的下标为7，且高度为0)

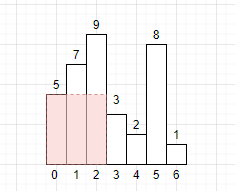
下标为1的柱子能形成的最大矩阵的面积为(3 - 0 - 1) * 7

标为2的柱子能形成的最大矩阵面积为(3 - 1 - 1 ) * 7 **， 这里也可以形成上图面积为14大小的矩阵，但是这样就重复计算了。

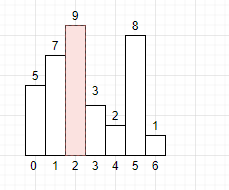
下标为3的柱子能形成的最大矩阵面积为(4 + 1 - 1 ) * 3

下标为4的柱子能形成的最大矩阵面积为(6 + 1 - 1 ) * 2

下标为5的柱子能形成的最大矩阵面积为(6 - 4 - 1 ) * 2

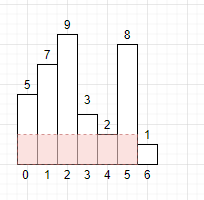
下标为6的柱子能形成的最大矩阵面积为(7 + 1 - 1 ) * 1

暴力法

根据上述结论 ，我们通过往左右分别找比当前柱子小的值就好 (根据LeetCode给出的测试数据，暴力法会TLE)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int ans = 0;
        for (int i = 0; i < heights.size(); ++i){
            int cur_h = heights[i];
            int j = 0, k = 0;
            // 往左找比当前柱子要小的柱子
            for (j = i - 1; j >= 0; j--)
                if (heights[j] < cur_h)    break;
             // 往右找比当前柱子要小的柱子
            for (k = i + 1; k < heights.size(); ++k)
                if (heights[k] < cur_h)    break;

            int cur_w = k - j - 1;
            ans = max(ans, cur_h * cur_w);
        }
        return ans;
    }
};

单调栈

既然我们需要在左右两个方向上找到比当前柱子更矮的柱子，那么我们能不能记录左边已经遍历过的柱子呢？

这个时候我们就想到单调栈 ==》 只存柱子高度递增的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        // 为了方便求解 我们在左右2个端点上插入高度为0的柱子
        int size = heights.size();
        vector<int> n_heights(size + 2, 0);
        for (int i = 0, j = 1; i < size; ++i, ++j)
            n_heights[j] = heights[i];
        
        stack<int> st;
        int ans = 0;
        for (int i = 0; i < n_heights.size(); ++i){
            while (!st.empty() && n_heights[st.top()] > n_heights[i]){
                // 进入循环说明 栈顶的元素要比当前遍历的柱子要高
                int cur_h = n_heights[st.top()];
                st.pop();
                // 当前栈顶的元素就是 左边比n_heights[i]要小的下标
                int cur_w = i - st.top() - 1;
                ans = max(ans, cur_w * cur_h);
            }
            st.push(i);
        }
        return ans;
    }
};