Trie(前缀树)

Posted on | In

通过刷题学习到的数据结构。

1. 什么是Trie

Trie树的名字有很多，比如字典树，前缀树等等。 如下图:

Trie

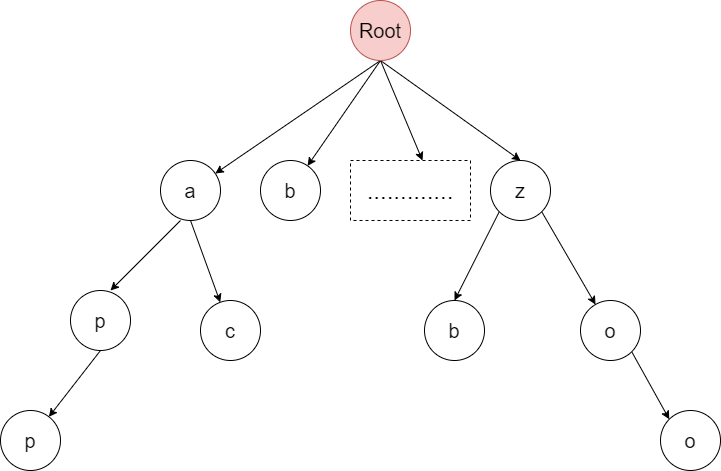
上图是一棵Trie，我们从上图已画出的节点来看，包含的集合有{“a”, “ap”,”app”, “ac”, “b”, “z”, “zb”, “zo”, “zoo”}

Trie的特点:

  1. 根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
  2. 从根节点到某一节点，路径上经过的字符连接起来，就是该节点对应的字符串。
  3. 每个单词的公共前缀作为一个字符节点保存。

通常会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

一般而言一个trie树的节点如果只统计小写的单词,那么它的节点需要有一个单词结尾的标志和26个孩子指针，其指针分别指向[a~z]。

2. Trie的作用

1. 词频统计。

可能有人会说，词频统计简单可以使用hash或者堆就可以逐个计数呀。但是这样会占用大量的空间，因为每个词都需要占用一定的空间。

如果内存有限呢？还能这么做吗？所以这里我们就可以通过使用Trie来压缩空间，因为公共前缀都是用一个节点保存的，这样就避免前缀的重复存储了，大大的节省了存储的空间。

2. 前缀匹配

就拿上面的图举例，如果我想获取所有以”a”开头的字符串，可以很快得到的是{“a”, “ap”, “app”, “ac”}，如果不用trie，该怎么做呢？

最直接的办法就是暴力匹配，时间复杂度为O(N^2) ，那么用Trie就不一样了，它可以做到len，len为检索单词的长度，可以说这样就大大提升了搜索的效率。

3. 字符串排序

Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。

正好leetcode上也有一道实现Trie的题目，连测试数据都不用写（窃喜）。

3. LeetCode 208

208. 实现 Trie (前缀树)

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。

示例:

1
2
3
4
5
6
7
8
9
> Trie trie = new Trie();
> 
> trie.insert("apple");
> trie.search("apple");   // 返回 true
> trie.search("app");     // 返回 false
> trie.startsWith("app"); // 返回 true
> trie.insert("app");   
> trie.search("app");     // 返回 true
>

说明:

  • 你可以假设所有的输入都是由小写字母 a-z 构成的。
  • 保证所有输入均为非空字符串。

思路: 上面已经通过性质说了很清楚了, 具体的细节我们在代码中通过注释的方式来说明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Trie {
public:
    /** Initialize your data structure here. */
    Trie():_root(new TrieNode()){}

    /** Inserts a word into the trie. */
    void insert(const string& word) {
        // 插入字符串
        // 获得_root的原始指针
        TrieNode* ptr = _root.get();
        for (auto c : word){
            // 若孩子节点中没有字符c则创建新的节点
            if (!ptr->child[c - 'a'])   ptr->child[c - 'a'] = new TrieNode();
            ptr = ptr->child[c - 'a'];
        }
        // 把字符串的最后个字符的标记置为true;
        ptr->is_word = true;
    }
    
    /** Returns if the word is in the trie. */
    bool search(const string& word) {
        auto p = find_str(word);
        return p && p->is_word;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(const string& prefix) {
        return find_str(prefix);
    }

private:
    class TrieNode{
    public:
        TrieNode():is_word(false), child(26, nullptr){};
        ~TrieNode(){
            // 节点的析构函数
            for (auto c : child)
                if (c)  delete c;
        };
        bool is_word;
        vector<TrieNode*> child; 
    };

    TrieNode* find_str(const string& s){
        TrieNode* ptr = _root.get();
        for (auto c : s){
            // 若孩子节点中不包括该字符就返回nullptr
            if (!ptr->child[c - 'a'])   return nullptr;
            // 若存在则沿着该字符继续向下寻找下个字符
            ptr = ptr->child[c - 'a'];
        }
        return ptr;
    }
    
    // 通过智能指针来定义根节点(不用手动delete)
    unique_ptr<TrieNode> _root;
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */