剑指Offer 44.数字序列中某一位的数字

Posted on | In

每次遇到这种找规律的题，我就很头疼…..咬咬牙还是坚持做完吧。

我相信下次我再遇到我依然不会做，所以我想把答案写的尽可能详细点，以便后期借此复习。

剑指 Offer 44. 数字序列中某一位的数字

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。

请写一个函数，求任意第n位对应的数字。

示例 1：

1
2
3
> 输入：n = 3
> 输出：3
>

示例 2： 

1
2
3
> 输入：n = 11
> 输出：0
>

限制：

  • 0 <= n < 2^31

思路是参考腐烂的橘子的思路一。

通过观察我们可以看到: 如下规律，1-9在一位数有9个数， 10-99两位数有99*2个数， 100-999三位数有900*3个数字，由此规律我们可以进一步知道1000-9999一共有9000 * 4个数字。

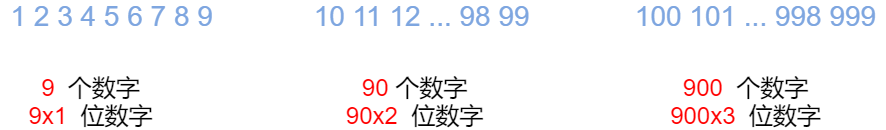
但是题目是从0开始的(埋下伏笔)，并不是从1开始的所以其实一位数上其实有10个数。

这个题目求解大概分为以下几个步骤:

  1. 确定数字n是几位数，并且求解n在第几位数上是排在第几个。
  2. 根据n_digits_pos计算出n是在哪个数字出现的，num = pow(10, digits - 1) + (n_digits_pos - 1) % digits。这里为什么n_digits_pos - 1呢? 是因为个位是从0开始的并不是从1开始的.
  3. 根据第二步我们算出了n出现在num中，现在我们需要确定是num中第几个数字。idx = (n_digits_pos - 1)% digits， 返回答案。

为了更好说明上面我们说到的步骤，我们来举一个具体的栗子。

我们以199为例。

  1. 199根据计算digits = 3， 排在第三位数中的n_digits_pos = (199 - 9 - 99 * 2 )位
  2. 计算n是在哪个数字中出现的，num = 10^(3-1) + (10 - 1) % 3(num的结果为100)
  3. idx = (10 - 1) % 3 ==> 结果为1, 我们可以得到我们的答案是1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findNthDigit(int n) {
        if (n < 10) return n;
        long long base = 9, digits = 1;
        long long n_digits_pos = n;
        while (n_digits_pos - base * digits > 0){
            n_digits_pos -= base * digits;
            base *= 10;
            digits ++;
        }

        long long num = (long long)pow(10, digits - 1) + (n_digits_pos - 1) / digits;
        long long idx = (n_digits_pos - 1) % digits;
        return to_string(num)[idx] - '0';
    }
};