这题是我个人感觉剑指offer里面最恶心的题目了,没有之一。
剑指 Offer 43. 1~n 整数中 1 出现的次数
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
2
3
> 输出:5
>
示例 2:
2
3
> 输出:6
>
限制:
1 <= n < 2^31
思路:是参考Huifeng Guan
给个具体点的例子来说明这个思路吧.
例如: 我们选取 41201
我们可以通过算得每位上出现1的次数累加之后就可以得到我们要的结果了
那么我们怎么算的每一位究竟有多少位1呢?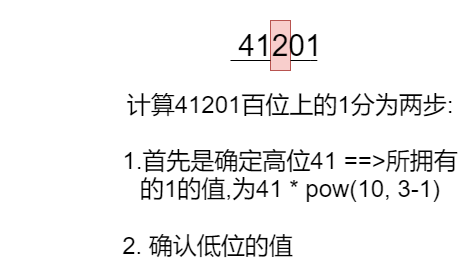
怎么确认低位的值呢?
分三种情况讨论
- 百位的值大于1, 那么个位和十位上所有的1都是您的! 那么低位共有 pow(3 - 1, 10)个1
- 百位的值等于1, 那么个位和十位上的1并不都是您的,只有小于 101的值是您的 所以一共有个1, 101中的百位上的1, 还有一个就是当前数字百位上的1
- 百位上的值等于0, 那么个位和十位上的1全都不是您的
这是讨论每个位上拥有的1的个数,同理 千位 万位上的1也是如此计算, 然后把所有的1累加起来就是答案.
1 | class Solution { |