常见排序汇总

Posted on | In

今天是个好日子，让我们把常见排序重新复习下。

所有动图源自：帅地

希尔排序原理讲解图源自:排序：希尔排序（算法）

冒泡排序

冒泡排序是交换排序的一种，它的思想非常简单：循环n次，每次通过比较挑选当前待排序列中的最大值，将其放置在队列的尾部。当某次循环没有进行交换时，说明当前序列是有序的，故完成排列。

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
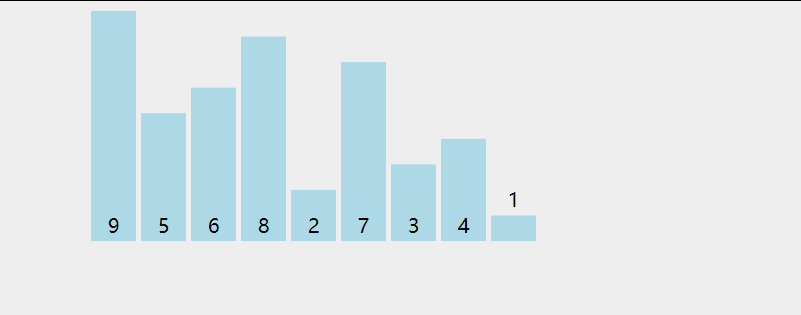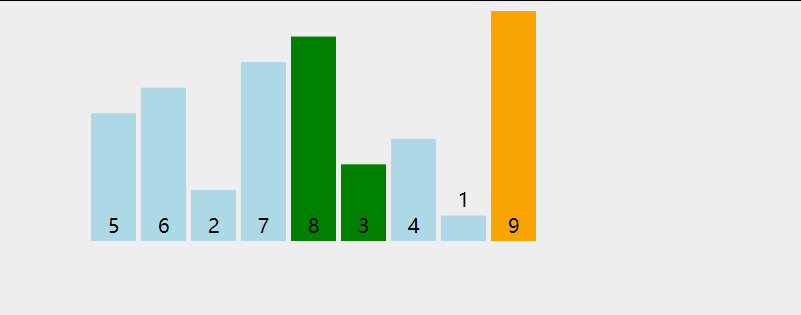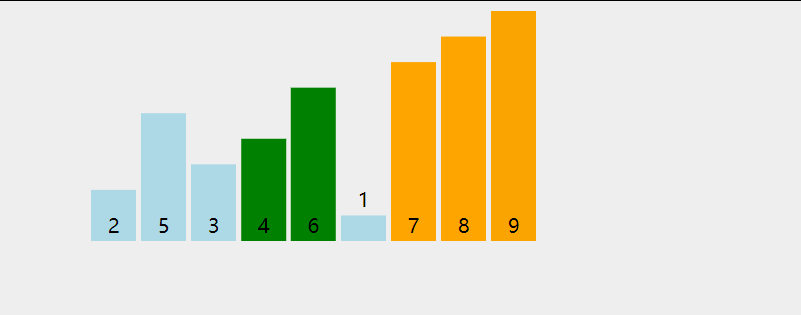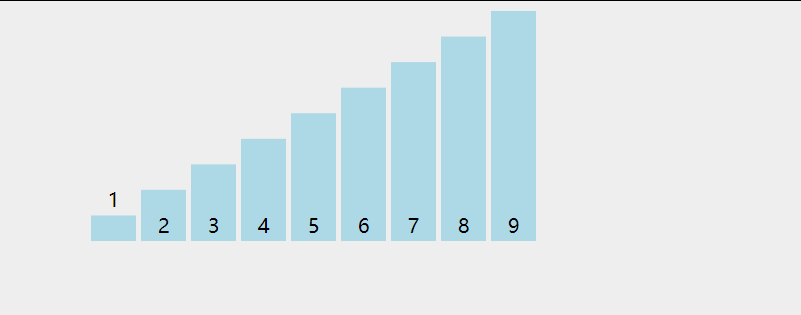
void bubble_sort(vector<int>& nums) {
    if (nums.empty() || nums.size() == 1)   return;
    // 冒泡排序通过交换,使得每次外循环结束之后都可以把当前数组未排序中的最大值交换到数组后部分
    bool flag = false;  // 优化冒泡排序 若某次没有进行交换说明 已经成功排序
    for (int i = 0; i < nums.size(); ++i) {
        for (int j = 1; j < nums.size() - i; ++j) {
            if (nums[j - 1] > nums[j]) {
                swap(nums[j - 1], nums[j]);
                flag = true;
            }
        }
        if (!flag) break;
    }
    return;
}

冒泡排序是一种稳定的排序算法。

时间复杂度为O(n^2)

选择排序

选择排序的思想很简单， 每趟遍历找到待排序列中最小的那个元素，将它和待排序列的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。如此往复，直到将整个序列排序。

下面的动图是每一趟选出最小值，而我们代码是每一趟选出最大值。

选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void select_sort(vector<int>& nums) {
    // 每趟都会选择出当前未选择的数组中的最大值
    // 并且与未排序数组中的最后一个元素交换位置
    if (nums.empty() || nums.size() == 1)   return;
    int len = nums.size();
    int cur_max = INT_MIN;
    int cur_max_pos = -1;
    for (int i = 0; i < len; ++i) {
        cur_max = INT_MIN;
        cur_max_pos = -1;
        for (int j = 0; j < len - i; ++j) {
            if (nums[j] > cur_max) {
                cur_max = nums[j];
                cur_max_pos = j;
            }
        }
        if (cur_max_pos == -1)  break;
        else 
            swap(nums[cur_max_pos], nums[len - i - 1]);
    }
    return;
}

选择排序是一种不稳定排序

时间复杂度为O(n^2)

插入排序

插入排序是算法导论的开门礼物，算法导论里面用将扑克捋顺的思路给我们讲解什么是插入排序。

过程其实很简单，就是维持一个有序序列，每次从待排序列的第一个元素插入到有序序列中，逐步的插入待排的序列，直到整个序列都有序。但是我们在代码中实现过程并不是用直接插入，而是用覆盖原有值的思想来替代直接插入的过程。

插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
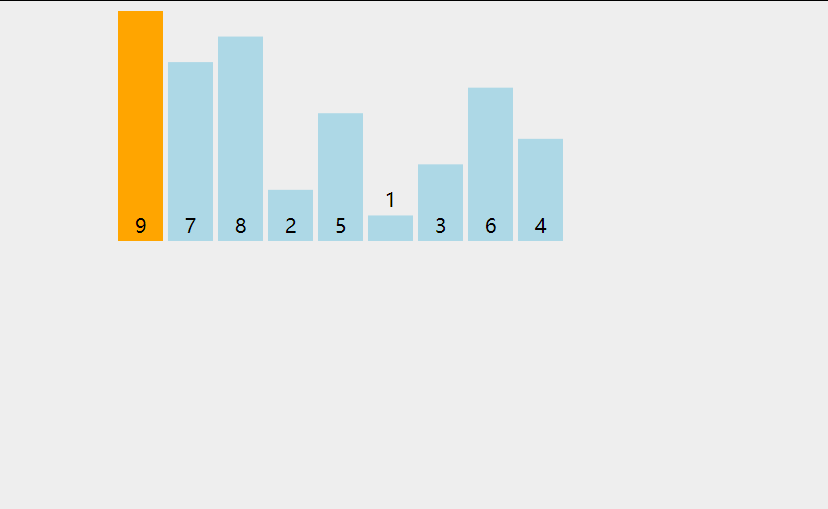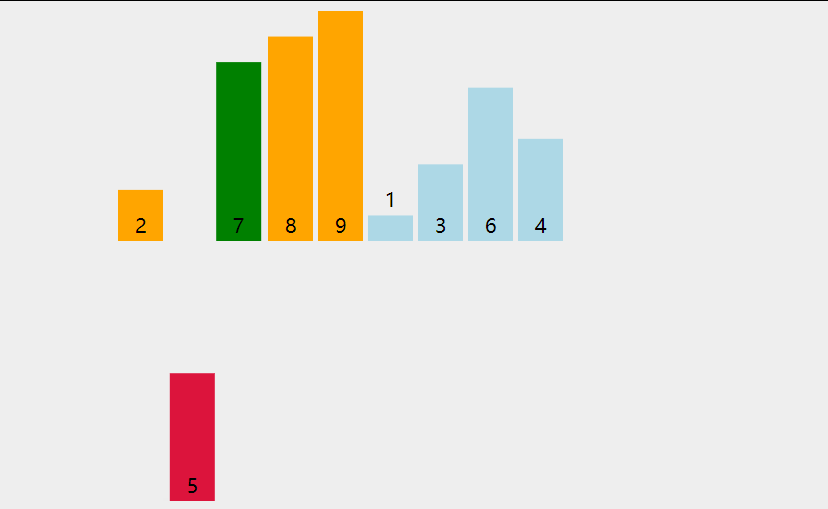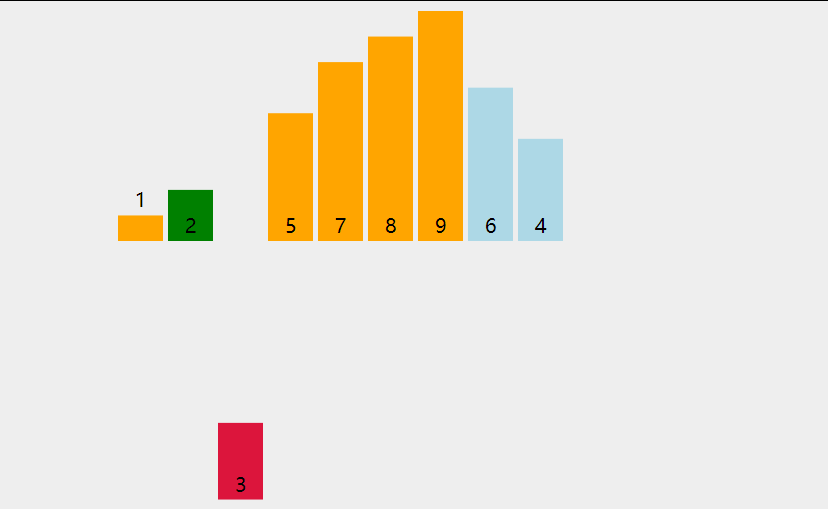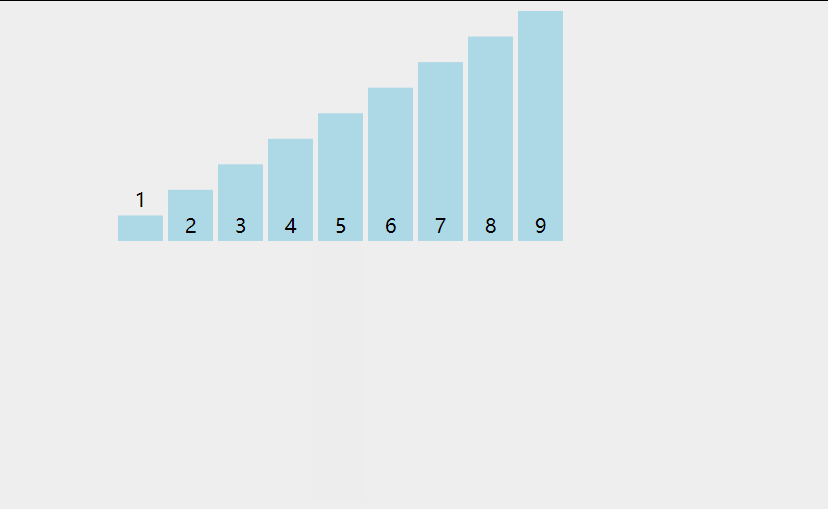
void insert_sort(vector<int>& nums) {
    if (nums.empty() || nums.size() == 1)   return;
    // 插入排序的思想是在数组前端维持一个有序序列, 将未排序的元素逐个的插入到已经有序的序列中
    int len = nums.size();
    for (int i = 1; i < len; ++i) {
        int j = i;
        int cur = nums[i];
        while (j > 0 && cur < nums[j - 1]) {
            nums[j] = nums[j - 1];
            j--;
        }
        nums[j] = cur;
    }
    return;
}

插入排序是一种稳定的排序。

时间复杂度为O(n^2)

希尔排序

希尔排序是一种特殊的插入排序，因为插入排序每一趟只能移动一个数据，所以是低效的。而希尔排序在插入基础上进行了改进。希尔排序首先将待排序序列按增量的长度分组，然后对每个分组进行插入排序（将每个分组看作成一个待排序列），最后逐渐缩减增量大小（一般逐次取一半）再重复上述过程，直至增量（h)为1时为最后一趟排序。

希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
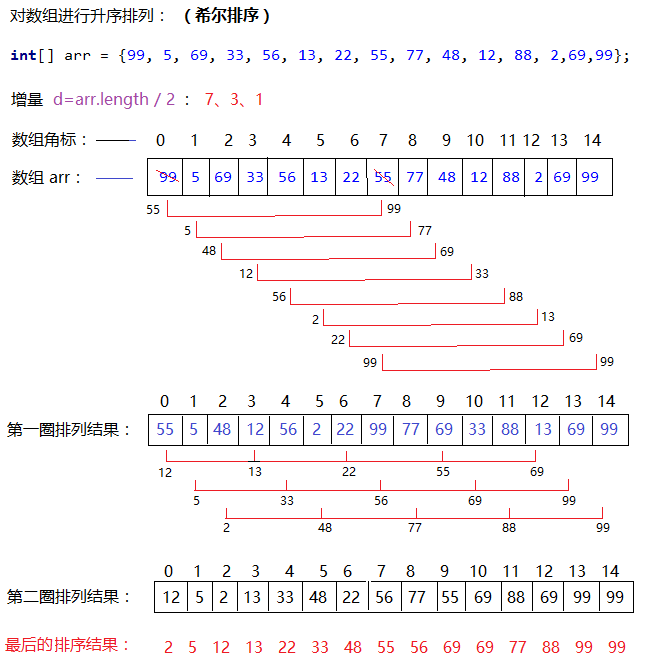
void shell_sort_helper(vector<int>& nums, int h) {
    int len = nums.size();
    // 将 [0, h) 中的元素视为已经有序的序列
    for (int i = h; i < len; ++i) {
    // 下面的代码就完全是插入排序的过程
        for (int j = i; j < len; j += h) {
            int k = j;
            int cur = nums[j];
            while (k >= h && cur < nums[k - h]) {
                nums[k] = nums[k - h];
                k -= h;
            }
            nums[k] = cur;
        }
    }
}

void shell_sort(vector<int>& nums) {
    /* 希尔排序是种特殊的插入排序,先让间隔为h的元素都有序,逐渐使得h的值变小,直到为1.
    *  一般来说h的取值为 h = 1 / 2 * length    
    *  h = 1 / 4 * length  h = 1 / 8 * length 直到 h == 1
    */
    if (nums.empty() || nums.size() == 1) return;
    int len = nums.size();
    for (int h = len / 2; h >= 1; h /= 2) {
        shell_sort_helper(nums, h);
    }
}

希尔排序是一种不稳定的排序。

时间复杂度为:

  1. 最好情况: O(n) 。当待排序列是正序排列，在这种情况下，需要进行的比较操作需（n-1）次。后移赋值操作为0次。
  2. 最坏情况: O(nlogn)
  3. 平均情况: O(nlogn)

快速排序

快速排序应该是所有排序中最负盛名的了。

快速排序基本上分三步完成：

  1. 在待排序列中选一个基准点(pivot)
  2. 将序列中小于基准点的数据移到左边,大于基准点的数移到右边
  3. 将基准点左右两个序列重复上述过程，只到序列的大小为1，即完成排序。

在快速排序算法中对于基准点选取对算法的影响是巨大的，因为基准点的选取决定了分割后两个子序列的长度。

最理想的方式是选择的基准点恰好能把待排序的序列分成两个等长的子序列。

一般来说选取基准点的方法有以下

  1. 选取固定的基准点：一般选取序列中第一个或最后一个元素，或则当前序列的中间元素。

  2. 选取随机选取基准点：通过随机函数，每次随机选取基准点。 这是一种相对安全的策略。由于枢轴的位置是随机的，那么产生的分割也不会总是会出现劣质的分割。 在整个数组数字全相等时，仍然是最坏情况，时间复杂度是O(n^2）。 所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn）的期望时间复杂度。一位前辈做出了一个精辟的总结：“随机化快速排序可以满足一个人一辈子的人品需求。”

  3. 三数取中： 通过随机选取三个元素并用它们的中值作为基准点而得到。

    例如待排序列为:[1, 7, 10, 2, 6, 9, 3, 5, 11, 16]

    选取了三次随机元素分别是: 9 3 11

    那么我们将选取9作为本次排序的基准点

另外：STL中的sort函数采用的就是快速排序 + 插入排序 + 堆排序的组合，当数据量大时采用快速排序，分段归并排序。一旦分段后的数据量小于某个门槛（16），为避免快排的递归调用带来过大的额外负荷，就改用插入排序。如果递归层次过深，还会改用堆排序。

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void quick_sort_handle(vector<int>& nums, int start , int end) {
    if (nums.empty() || nums.size() == 1)   return;
    if (start >= end) return;
    int l = start, r = end;
    // pivot_pos 取当前数组[start, end]之间的随机某个位置
    // rand() 通用公式  a + rand() % n 
    // 其中的a是起始值, n是整数的范围
    int pivot_pos = (rand() % (end - start + 1)) + start;
    int pivot = nums[pivot_pos];
    while (l <= r) {
        while (l <= r && nums[l] < pivot) l++;
        while (l <= r && nums[r] > pivot) r--;
        if (l <= r) {
            swap(nums[l], nums[r]);
            l++;
            r--;
        }
    }
    quick_sort_handle(nums, start, r);
    quick_sort_handle(nums, l, end);
}

void quick_sort(vector<int>& nums) {
    if (nums.empty() || nums.size() == 1)   return;
    quick_sort_handle(nums, 0, nums.size() - 1);
}

快速排序是一种不稳定 的排序算法。

理想的情况是，每次划分所选择的中间数恰好将当前序列几乎等分，经过log2n趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为O(nlog2n)。

最坏的情况是，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为O(n2)。

归并排序

归并排序分为两步

  1. 拆分序列, 直至每组序列只有1个元素
  2. 两两合并序列,再合并的过程中使每个新的序列有序

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
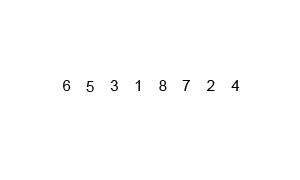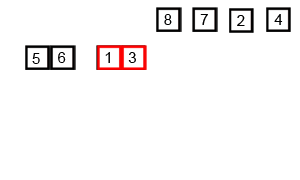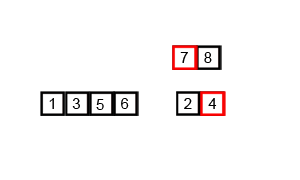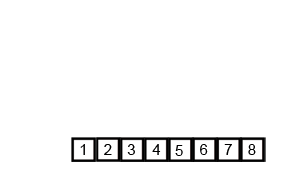
void merge(vector<int>& nums, int left, int mid, int right) {
    // merge的过程其实就是一个打擂台的算法
    // 把小区间通过打擂台的方式排好序
    vector<int> tmp(right - left + 1, 0);
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right) {
        // 这里一定要是 <= 如果不是的话归并排序就是不稳定排序了
        if (nums[i] <= nums[j])
            tmp[k++] = nums[i++];
        else
            tmp[k++] = nums[j++];
    }
    while (i <= mid)    tmp[k++] = nums[i++];
    while (j <= right)  tmp[k++] = nums[j++];

    // 将排好序的临时vector中的数组复制到原数组
    for (int i = 0, j = left; i < tmp.size(); ++i, ++j)
        nums[j] = tmp[i];
}

void merge_sort_handle(vector<int>& nums, int left, int right) {
    if (nums.empty() || nums.size() == 1)   return;
    if (left >= right) return;
    int mid = left + (right - left) / 2;
    merge_sort_handle(nums, left, mid);
    merge_sort_handle(nums, mid + 1, right);
    merge(nums, left, mid, right);
}

void merge_sort(vector<int>& nums) {
    if (nums.empty() || nums.size() == 1)   return;
    merge_sort_handle(nums, 0, nums.size() - 1);
}

归并排序是一种稳定的算法.

时间复杂度为O(nlogn)

堆排序

由于我们之前已经对堆排序做了详细的介绍了，就不在赘述了。

常见排序:堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void heapfiy(vector<int>& nums, int start, int n) {
    // 将当前堆调整为大顶堆
    if (start >= n) return;
    int left_child =start * 2 + 1;
    int right_child =start * 2 + 2;
    // 找出 父子节点中最大值
    int max_idx = start;
    if (left_child <= n && nums[left_child] >= nums[max_idx])
        max_idx = left_child;
    if (right_child <= n && nums[right_child] >= nums[max_idx])
        max_idx = right_child;
    // 如果最大值不是父节点, 将其与子节点交换并递归的调整交换过的节点
    if (max_idx != start) {
        swap(nums[start], nums[max_idx]);
        heapfiy(nums, max_idx, n);
    }
}

void build_heap(vector<int>& nums) {
    // 建堆要从倒数第二层开始建
    int size = nums.size() - 1;
    int parent = size / 2 - 1;
    for (int i = parent; i >= 0; --i)
        heapfiy(nums, i, size);
}

void heap_sort(vector<int>& nums) {
    if (nums.empty() || nums.size() == 1)   return;
    build_heap(nums);
    for (int i = nums.size() - 1; i >= 0; --i) {
        // 每次把最大值都放到数组的队尾,然后逐步缩小堆的范围.
        swap(nums[0], nums[i]);
        heapfiy(nums, 0, i - 1);
    }
}

计数排序

计数排序一般来说只适合数据范围不太大的排序(因为数据的上下限决定着哈希表的大小,太大容易爆栈)

思路其实很简单:就是把待排的数组中的元素都映射都哈希表中,哈希表key表示待排元素的值,val表示值出现的次数

计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
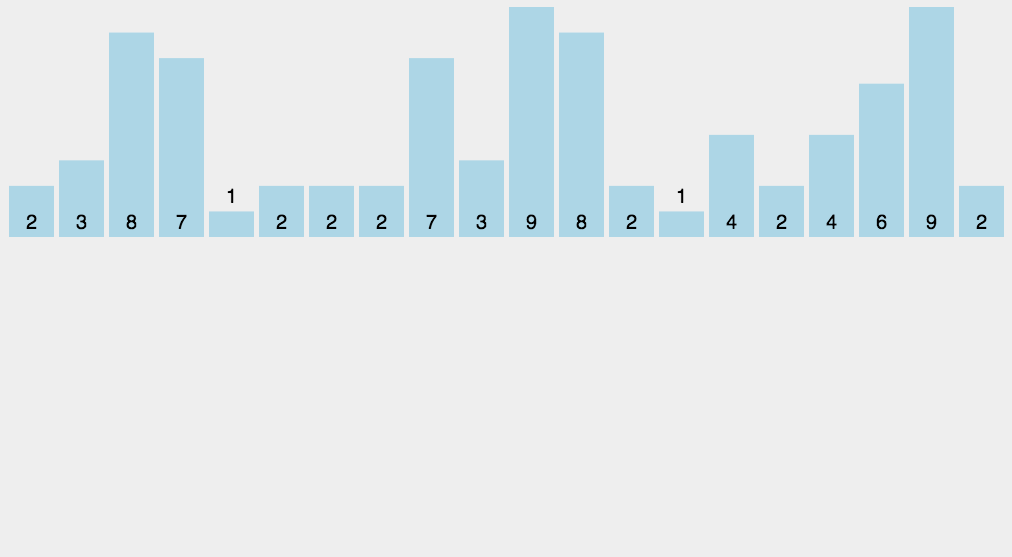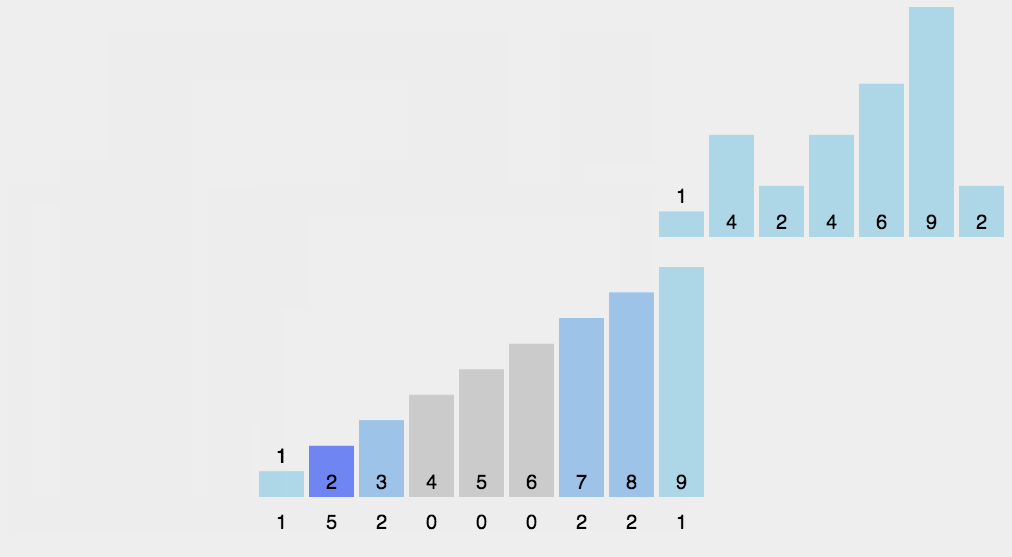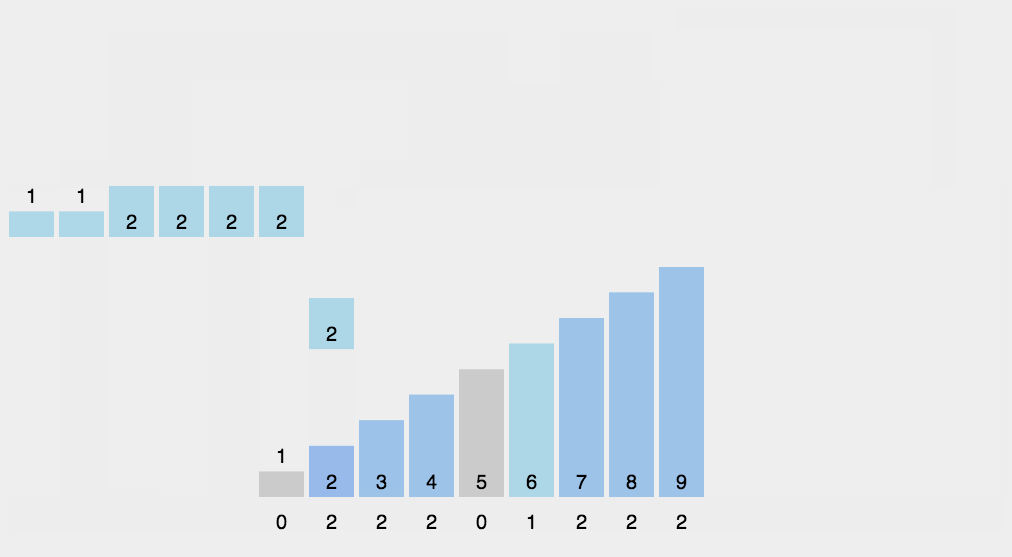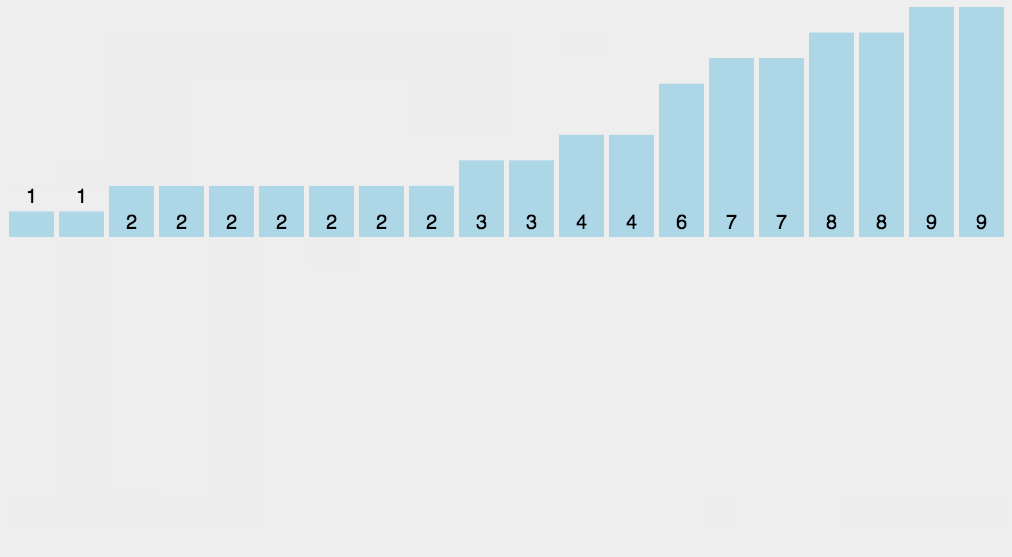
void cnt_sort(vector<int>& nums) {
    // 计数排序一般来说只适合数据范围不太大的排序(因为数据的上下限决定着哈希表的大小,太大容易爆栈)
    // 思路其实很简单:就是把待排的数组中的元素都映射都哈希表中,哈希表key表示待排元素的值,val表示值出现的次数
    if (nums.empty() || nums.size() == 1)   return;
    int nums_min = INT_MAX, nums_max = INT_MIN;
    for (const auto& i : nums) {
        if (nums_min > i) nums_min = i;
        if (nums_max < i) nums_max = i;
    }
    // 哈希表的长度
    int diff = nums_max - nums_min + 1;
    int size = nums.size();
    // 一个简单的哈希表
    vector<int> _count(diff, 0);       

    int dist = 0 - nums_min;
    // 将待排序列的元素存储到哈希表中
    for (int i = 0; i < size; ++i)
        _count[nums[i] + dist]++;
    
    for (int i = 0, idx = 0; i < _count.size(); ++i) {
        while (_count[i]) {
            nums[idx++] = i - dist;
            _count[i]--;
        }
    }
    return;
}

计数排序是一种稳定的算法.

时间复杂度：O(n)