LeetCode 295.数据流中的中位数

Posted on | In

数据流?

295. 数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

  • void addNum(int num) - 从数据流中添加一个整数到数据结构中。

  • double findMedian() - 返回目前所有元素的中位数。

    示例： 

1
2
3
4
5
6
> addNum(1)
> addNum(2)
> findMedian() -> 1.5
> addNum(3) 
> findMedian() -> 2
>

数据流：数据流是指一组有顺序的、有起点和终点的字节集合，程序从键盘接收数据或向文件中写数据，以及在网络连接上进行数据的读写操作，都可以使用数据流来完成。

一般而言我们无法得到数据流的长度，所以不能将数据流进行排序然后输出中间数，得到答案。(LC直接排序也会TLE)

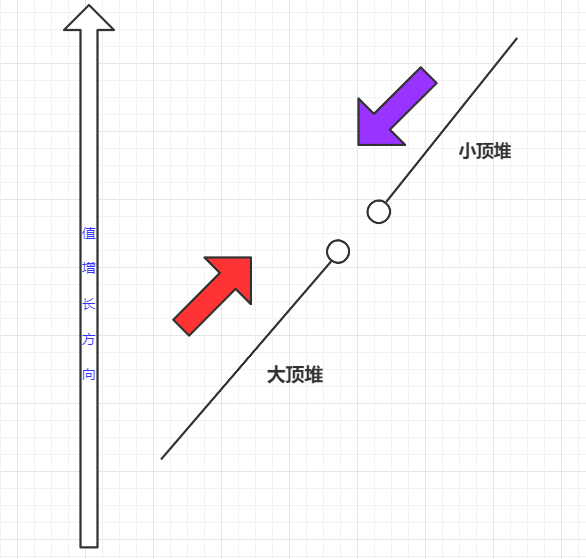
算法思想：维持一个最大堆和最小堆。依次向最大堆和最小堆中插入元素。插入过程中要保证最大堆的堆顶元素始终小于最小堆的堆顶元素。 比如，当前要向最小堆插入元素，但是该元素小于最大堆的堆顶元素，则从最大堆中pop出堆顶元素，将该元素插入到最大堆。将pop出的堆顶元素插入到最小堆。 根据奇偶性，返回堆顶元素或者两个堆顶元素的平均值。

大概的样子如下图所示.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class MedianFinder {
public:
    /** initialize your data structure here. */
    MedianFinder() {
        _maxsize = 0;
        _minsize = 0;
    }
    
    void addNum(int num) {
        if (_minsize == 0){
            _minheap.push(num);
            _minsize++;
        }
        else if (_maxsize == 0){
            // 如果插入的时候大顶堆为空,且插入的值比小顶堆的堆顶要大
            // 交换两个值, 始终保证小顶堆中的值要大于大顶堆
            if (num > _minheap.top()){
                _minheap.push(num);
                _maxheap.push(_minheap.top());
                _minheap.pop();
            }
            else
                _maxheap.push(num);
            _maxsize++;
        }
        else{
            if (num > _minheap.top()){
                _minheap.push(num);
                _minsize++;
            }
            else{
                _maxheap.push(num);
                _maxsize++;
            }
        }
        // 为了保证大顶堆和小顶堆的规模大小差值在1之类,所以要检查是否需要调整
        balance();
    }
    void balance(){
        if (abs(_maxsize - _minsize) <= 1)  return;
        if (_maxsize > _minsize){
            _minheap.push(_maxheap.top());
            _maxheap.pop();
            _minsize++;
            _maxsize--;
        }
        else{
            _maxheap.push(_minheap.top());
            _minheap.pop();
            _maxsize++;
            _minsize--;
        }
    }
    
    double findMedian() {
        if (_minsize > _maxsize)    return _minheap.top();
        if (_maxsize > _minsize)    return _maxheap.top();
        return static_cast<double>(_maxheap.top() + _minheap.top()) / 2;
    }

private:
    priority_queue<int, vector<int>, greater<int>> _minheap;
    priority_queue<int, vector<int>, less<int>> _maxheap;
    int _maxsize;
    int _minsize;
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */