LeetCode 162.寻找峰值

Posted on | In

162. 寻找峰值

峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

示例 1: 

1
2
3
4
> 输入: nums = [1,2,3,1]
> 输出: 2
> 解释: 3 是峰值元素，你的函数应该返回其索引 2。
>

示例 2: 

1
2
3
4
5
> 输入: nums = [1,2,1,3,5,6,4]
> 输出: 1 或 5 
> 解释: 你的函数可以返回索引 1，其峰值元素为 2；
>      或者返回索引 5， 其峰值元素为 6。
>

说明:

你的解法应该是 O(logN) 时间复杂度的。

思路:说明给出了时间复杂度是O(logN)这是个很明显的二分查找法的提示.

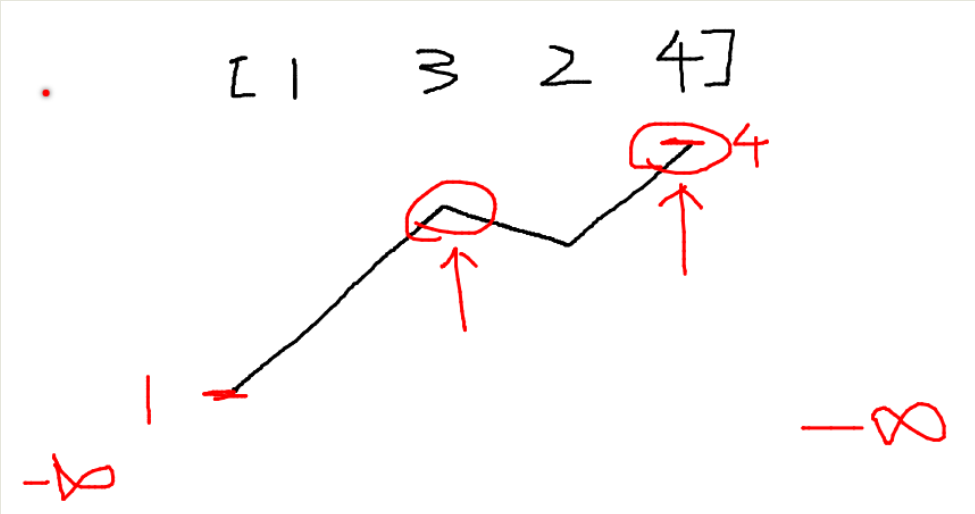
上图给出了数组是[1, 3, 2, 4],其中被红箭头标记的值为3和值为4的点都是峰值

我们可以通过二分法通过比较nums[mid] 和nums[mid - 1]或(nums[mid + 1])来判断数组变化的方向.

例如我们这里选用的是nums[mid]和(nums[mid + 1])

  1. nums[mid] < (nums[mid + 1]) 数组在局部是递增的,峰值可能在 mid + 1或则 大于mid + 1的位置
  2. nums[mid] > (nums[mid + 1]) 数组在局部是递减的,峰值可能在 mid或则 小于mid的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        // 二分法
        int size = nums.size();
        if (size == 0)  return 0;
        int l = 0, r = size - 1;
        while ( l < r){
            int m = l + (r - l) / 2;
            if (m + 1 < size && nums[m] < nums[m + 1]) l = m + 1;
            else    r = m;
        }
        if (nums[l] > nums[r])  return l;
        return r;
    }
};