LeetCode-116.填充每个节点的下一个右侧节点指针

Posted on | In

巧妙的算法化解空间复杂度.

116. 填充每个节点的下一个右侧节点指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

输入：{“$id”:”1”,”left”:{“$id”:”2”,”left”:{“$id”:”3”,”left”:null,”next”:null,”right”:null,”val”:4},”next”:null,”right”:{“$id”:”4”,”left”:null,”next”:null,”right”:null,”val”:5},”val”:2},”next”:null,”right”:{“$id”:”5”,”left”:{“$id”:”6”,”left”:null,”next”:null,”right”:null,”val”:6},”next”:null,”right”:{“$id”:”7”,”left”:null,”next”:null,”right”:null,”val”:7},”val”:3},”val”:1}

输出：{“$id”:”1”,”left”:{“$id”:”2”,”left”:{“$id”:”3”,”left”:null,”next”:{“$id”:”4”,”left”:null,”next”:{“$id”:”5”,”left”:null,”next”:{“$id”:”6”,”left”:null,”next”:null,”right”:null,”val”:7},”right”:null,”val”:6},”right”:null,”val”:5},”right”:null,”val”:4},”next”:{“$id”:”7”,”left”:{“$ref”:”5”},”next”:null,”right”:{“$ref”:”6”},”val”:3},”right”:{“$ref”:”4”},”val”:2},”next”:null,”right”:{“$ref”:”7”},”val”:1}

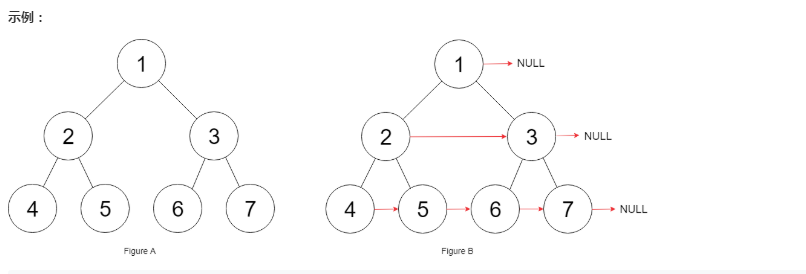
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

第一反应就是采用层次遍历(BFS)来逐个的给节点添加next指针，但是题目要求了是原地算法（常数的空间复杂度）这样就要打消这个思路了。

仔细观察我们可以发现由于所有next初始化都是为null，我们只需要处理相对来说左边节点且有next节点的节点，这样就可以分为

  1. 亲兄弟节点: 很好找根节点左孩子的next节点就是右孩子, 右孩子next为NULL不需要处理
  2. 堂兄弟节点: 如上图5的next节点是6，需要通过5的父节点找到6的父节点.
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    Node* connect(Node* root) {
        if (!root)  return nullptr;
        // 1. 亲兄弟
        if (root->left) root->left->next = root->right;
        // 2. 堂兄弟 root->next 为堂兄弟的父节点
        if (root->next && root->right) root->right->next = root->next->left;
        connect(root->left);
        connect(root->right);
        return root;
    }
};