LeedCode-全排列

Posted on | In

全排列是dfs中一个典型的问题，本文可以作为permutation问题的模板代码作为使用。

46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

1
2
3
4
5
6
7
8
9
10
> 输入: [1,2,3]输出:
> [
>   [1,2,3],
>   [1,3,2],
>   [2,1,3],
>   [2,3,1],
>   [3,1,2],
>   [3,2,1]
> ]
>

思路

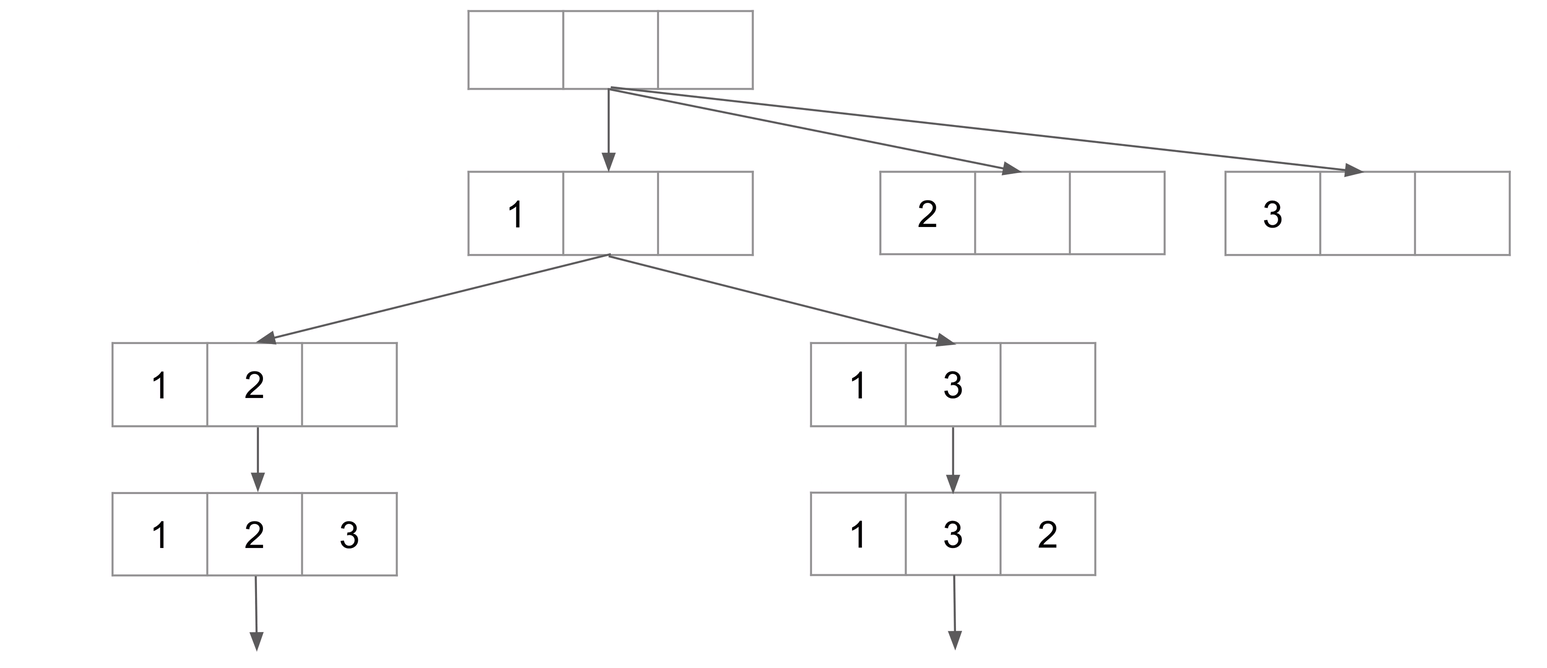
可以将待选数组看做成一个数据集，每次挑选的时候要判断挑选的数是否被已经被使用过，如果被使用过则选下一个未被使用的数字。例如从空集开始挑选数字，选择数字1，第二次继续选择的时候就不能选数字1，只能选取2和3，这是怎么实现的呢？是通过一个记录遍历过字符的数组实现，将当前已经使用过的元素进行标记，这也是permutation问题求解的关键。然后需要递归的去找取剩下的组合。

先有个模糊的概念，然后再来看看代码吧，代码胜千言。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
 class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ans;
        vector<int> cur;
        vector<bool> visited(nums.size(), false);	//标记元素是否使用过
        dfs(nums, ans, cur, visited);
        return ans;
    }

    void dfs(vector<int>& nums, vector<vector<int>>& ans, vector<int>& cur, vector<bool>& visited){
        if(cur.size() == nums.size()){
            ans.emplace_back(cur);
            return;
        }
        for(int i = 0; i < nums.size(); ++i){
            if(!visited[i]){				// 若该次未使用则挑选
                visited[i] = true;
                cur.emplace_back(nums[i]);
                dfs(nums, ans, cur, visited);
                cur.pop_back();				//恢复现场
                visited[i] = false;
            }
        }
    }
};

47. 全排列 II

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

1
2
3
4
5
6
7
8
> 输入: [1,1,2]
> 输出:
> [
>   [1,1,2],
>   [1,2,1],
>   [2,1,1]
> ]
>

47题和46题最大的区别是数据集合中可以出现重复的元素，这样就会导致生成的排列中有重复的排列。

示例：

1
2
3
输入:"112"
预期："121,112,211"
若不去重则输出: "112,121,112,121,211,211"

ps:下图来源LeetCode liweiwei1419视频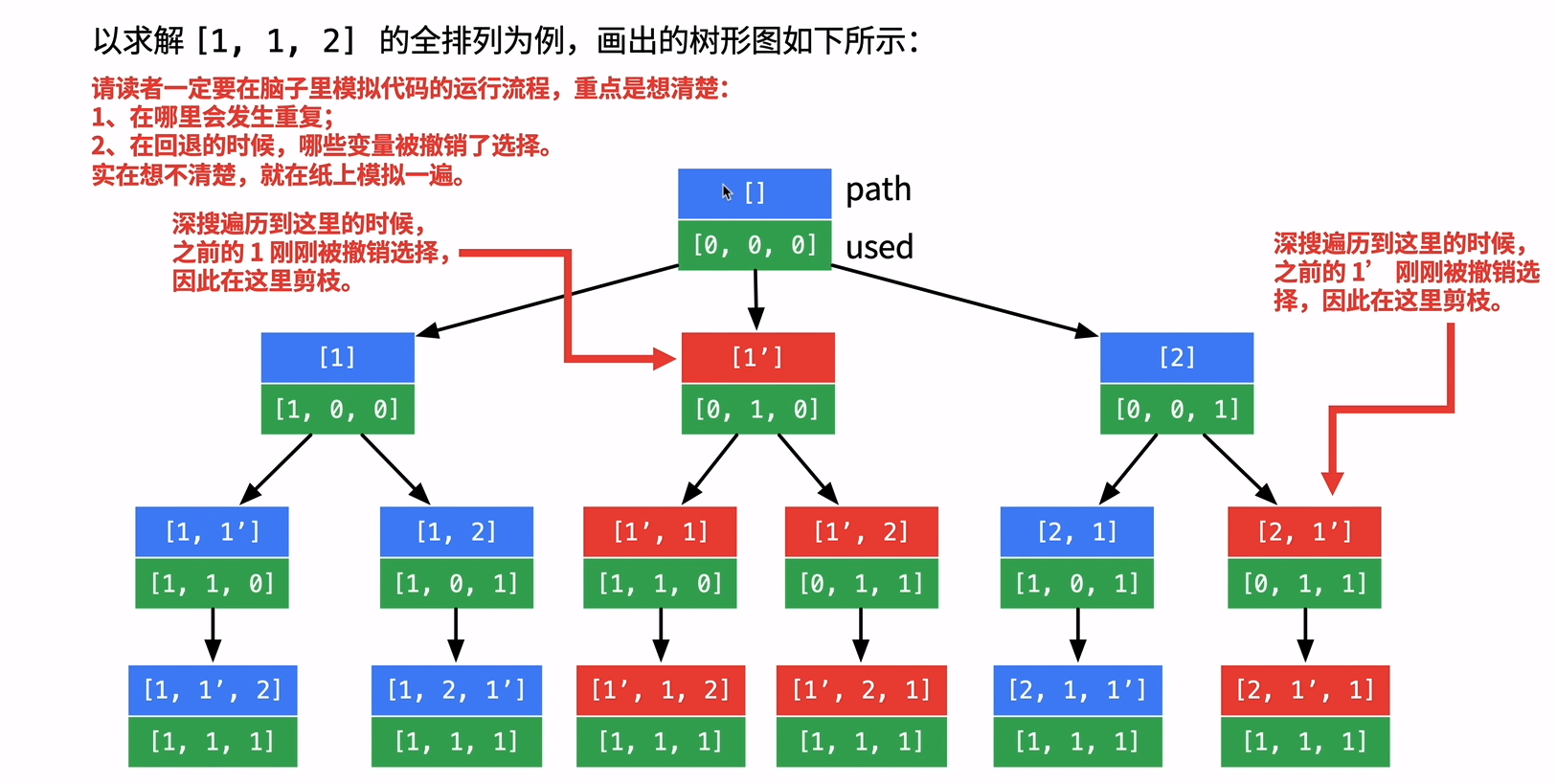

如果出现两个重复的数，在进行全排列的时候就会出现重复集合，所以处理去重的时候看上图可知重复的为红色标注。想要把中间那个递归树去除掉只需要用

1
2
if(i > 0 && nums[i] == nums[i - 1])
    countine;

但是仅仅是上面的条件就会把1选成[1，1]给去除掉，由观察可以看出如果上述条件成立下，还要使得前面说的[1，1]能够保留下来，需判断visited[i - 1] == true则可以选。

综上所述去重的核心代码

1
2
if(i > 0 && nums[i] == nums[i - 1] && nums[i-1] == false)
    countine;

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        vector<int> cur;
        vector<bool> visited(nums.size(), false);
        dfs(nums, ans, cur, visited);
        return ans;
    }
    void dfs(vector<int>& nums, vector<vector<int>>& ans, vector<int>& cur, vector<bool>& visited) {
        if (cur.size() == nums.size()) {
            ans.emplace_back(cur);
            return;
        }
        for (int i = 0; i < nums.size(); ++i) {
            if (!visited[i]) {
                if (i > 0 && nums[i] == nums[i - 1] && !visited[i - 1])
                    continue;
                visited[i] = true;
                cur.emplace_back(nums[i]);
                dfs(nums, ans, cur, visited);
                cur.pop_back();
                visited[i] = false;
            }
        }

    } 
};